Tốt nghiệp kỹ sư điện tử trường đại học danh giá Stanford, lấy bằng tiến sĩ vật lý tại viện kỹ thuật hàng đầu thế giới Caltech với luận án về laser bán dẫn, hoàn tất chương trình hậu tiến sĩ, Robert Lang trở thành nhà nghiên cứu tài năng về sợi quang học. Từng làm việc cho NASA và những phòng thí nghiệm danh tiếng khác, Lang là tác giả hay đồng tác giả của hơn 80 công trình nghiên cứu về laser bán dẫn, quang học, quang điện tử; ông cũng đang giữ 46 bằng sáng chế trong những lĩnh vực này. Thú vui của Lang là xếp giấy (origami).
Năm 2001, ở tuổi 40, Lang từ bỏ công việc mà nhiều người mơ ước để dành toàn thời gian cho nghệ thuật xếp giấy. Hẳn bạn cho rằng hành động của Lang thật là kỳ quái, vì xếp giấy thì có đáng gì để theo đuổi. Nhưng Lang cho rằng, có rất nhiều người đang làm việc về laser, nhưng nhiều công việc trong lĩnh vực xếp giấy nếu ông không dành toàn tâm thì sẽ không thể giải quyết.
Năm học lớp một, cô giáo của Lang đã tặng ông một cuốn sách nghệ thuật xếp giấy, với hy vọng những thách thức của origami sẽ khiến cậu bé bận rộn và không quấy rối các bạn cùng lớp. Cô đã không sai khi Lang tìm thấy niềm say mê trong thú vui mới, nhưng cô không ngờ rằng, với từng nếp gấp của chiếc máy bay, chú hạc thì Lang ngày càng tiến gần đến việc khám phá những bí ẩn của nghệ thuật origami và trở thành nhà sáng chế trong những lĩnh vực như phi thuyền không gian, giải phẫu tim và công nghiệp ô tô.
Lang đã thấy gì trong môn nghệ thuật cổ xưa này của Nhật mà người khác không nhìn thấy? Đó chính là hình mẫu (patterns). Khi bạn thấy được những hình mẫu thì có thể giải quyết những vấn đề của mình trong lĩnh vực nào đó nhờ vào tri thức của nhân loại đã được tích lũy ở những lĩnh vực khác.
Origami chỉ "đơn giản" là những đường gấp, hay nói văn vẻ là bản vẽ kỹ thuật của một tác phẩm. Tất nhiên, chúng ta không thể tùy tiện vẽ chúng mà phải tuân thủ bốn quy tắc căn bản. Quy tắc đầu tiên là tô hai màu, nghĩa là bạn có thể tô bất cứ mẫu gấp nào bằng hai màu mà không có các ô cạnh nhau trùng màu. Thứ hai là tại bất kỳ giao điểm nào - số nếp gấp cao (mountain fold) và số nếp gấp sâu (valley fold) luôn chênh nhau hai đơn vị (hơn hai hay kém hai). Nếu bạn nhìn vào các góc quanh một nếp gấp, thì khi đánh số các góc theo vòng tròn, thì tổng tất cả góc số chẵn và tổng tất cả góc số lẻ đều là 180 độ. Và cuối cùng, nếu nhìn cách các lớp chồng lên nhau, bạn sẽ nhận thấy rằng, cho dù những nếp gấp và lớp giấy chồng lên nhau như thế nào chăng nữa thì tấm giấy không bao giờ đi xuyên qua một nếp gấp. Vậy đó, toàn bộ hình gấp origami đều tuân theo 4 quy tắc này, và từ đây có thể làm nên những điều kỳ diệu.
Năm 1987, khi còn là nghiên cứu sinh sau tiến sĩ, Lang và vợ do say mê đồng hồ quả lắc với chú chim cu báo giờ nên đã dành ra 3 tháng để thiết kế và 6 giờ gấp từ một tờ giấy vuông, không cắt, để cho ra đời tác phẩm như bên dưới. (Hình 1)
Là một nhà khoa học, Lang dần nhận ra rằng mọi mẫu origami đều tuân theo một số hình mẫu nhất định. Ông đã phát triển một phần mềm chuyên dụng (TreeMaker) dựa trên các giải thuật và lý thuyết của nhiều ngành toán. TreeMaker hiện đã có phiên bản 5.0, cho phép tính toán tất cả mẫu xếp của bất kỳ hình ảnh nào bạn tưởng tượng được, ví dụ cho con bọ cánh cứng dưới đây: | | 
Hình 1: Đồng hồ quả lắc với chú chim cu báo giờ "Black Forest cuckoo clocks" được Lang gấp năm 1987. |

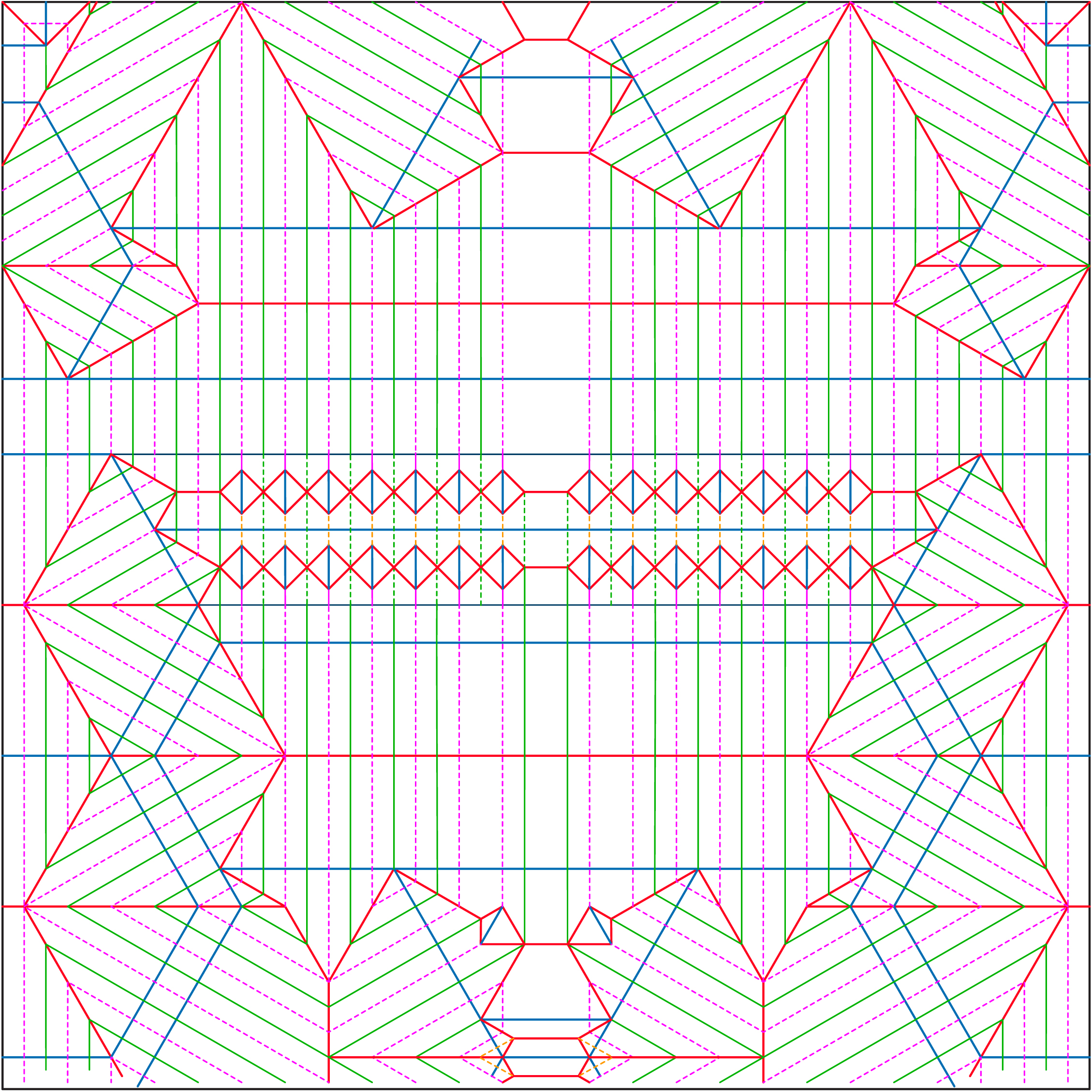
Chú bọ cánh cứng và thiết kế mẫu để gấp.
Bạn có thể tìm hiểu về phần mềm thiết kế cũng như tải về phiên bản mới nhất miễn phí trên website của Lang:
http://www.langorigami.com/science/computational/treemaker/treemaker.php.
Với phần mềm này bạn chỉ cần đưa bất kỳ hình ảnh nào mình muốn gấp ở dạng tối giản hình que và sẽ được sơ đồ gấp như trên. Tuy đôi lúc sơ đồ không thể gấp được, mà bạn phải tinh chỉnh lại bằng tay và có thể lồng sự sáng tạo của mình vào đó. Tuy nhiên, nó là một công cụ mạnh mẽ để phác họa cực nhanh.
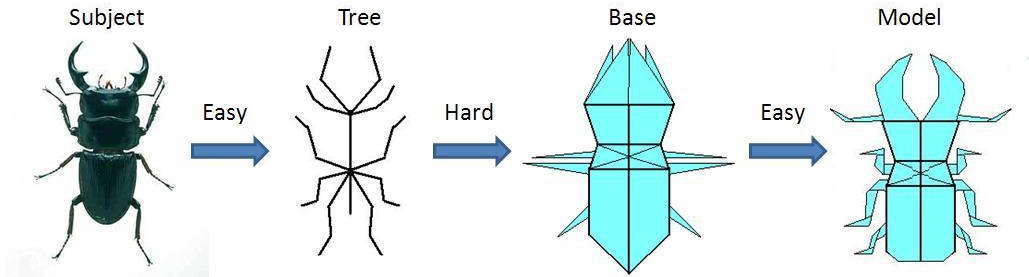
Đối tượng bất kỳ muốn gấp được trừu tượng hóa ở dạng tối giản hình que
và đưa vào TreeMaker để tạo sơ đồ gấp.
Vậy, những nội dung như trên có liên quan gì đến các ứng dụng trong đời sống? Koryo Miura, một kỹ sư người Nhật đã nghiên cứu và sáng tạo ra kiểu gấp mang tên ông "Miura-ori" như trong hình, có thể gấp lại cực kỳ nhỏ gọn và điểm đặc biệt là cấu trúc đóng, mở rất đơn giản. Kiểu gấp này đã được ứng dụng để thiết kế tấm pin mặt trời cùng bay vào vũ trụ với kính thiên văn Nhật Bản vào năm 1995.

Kiểu gấp "Miura-ori" được ứng dụng để thiết kế tấm pin mặt trời năm 1995.
Trong không gian còn có những origami khác: cơ quan thám hiểm không gian Nhật Bản đã phóng "cánh buồm mặt trời" (solar sail). Bạn có thể thấy cánh buồm mở ra, và thậm chí là những đường gấp.

"Cánh buồm mặt trời" (solar sail) được Nhật Bản phóng vào vũ trụ.
Tuy nhiên, vấn đề quan trọng hơn là giải được bài toán: làm sao để một đối tượng đủ nhỏ ở điểm xuất phát, nhưng trở nên to lớn và liền lạc tại đích đến. Bạn tưởng chỉ đi vào vũ trụ mới gặp thách thức đó ư? Những ống nong mạch máu (stent) cho tim do Zhong You, Đại học Oxford phát triển, có thể gấp lại nhờ một kiểu gấp origami đạt đường kính 12 mm và khi bung ra ở điểm cần nong đạt đường kính 23 mm.
Một hãng xe hơi nổi tiếng của Đức khi gặp vấn đề trong việc gấp các túi an toàn (airbag) cho loại xe cao cấp, họ đã phải nhờ đến Lang. Thuật toán mà ông phát triển để xếp côn trùng trở thành giải pháp cho việc xếp những chiếc túi này trong các mô phỏng trên máy tính của hãng. Những đường gấp của origami đã giúp "thu gọn" chiếc túi trong một không gian nhỏ nhất nhưng cho phép nó bung ra chỉ trong vài phần nghìn giây.
Nhóm nghiên cứu của Lawrence Livermore National Laboratory muốn chế tạo và đưa vào không gian kính thiên văn có ống kính với đường kính 100 m (nghĩa là lớn gấp 40 lần kính Hubble, đường kính chỉ 2,4 m) trong khi tên lửa vận chuyển chỉ cho phép mang những ống hình trụ đường kính từ 3-5 m mà thôi. Lời giải cho bài toán đưa kính thiên văn đường kính cỡ này lên độ cao khoảng 40.000 km được Lang phối hợp giải quyết bằng origami! Kính thiên văn Eyeglass với đường kính 100 m được "gấp lại" gọn trong 1 tên lửa đường kính từ 3-5 m bằng kiểu gấp dù (umbrella) của origami để gấp những hình tròn lớn thành khối hình trụ nhỏ hơn, khi phóng lên quỹ đạo sẽ bung ra ở kích thước thật. (Hình 2)
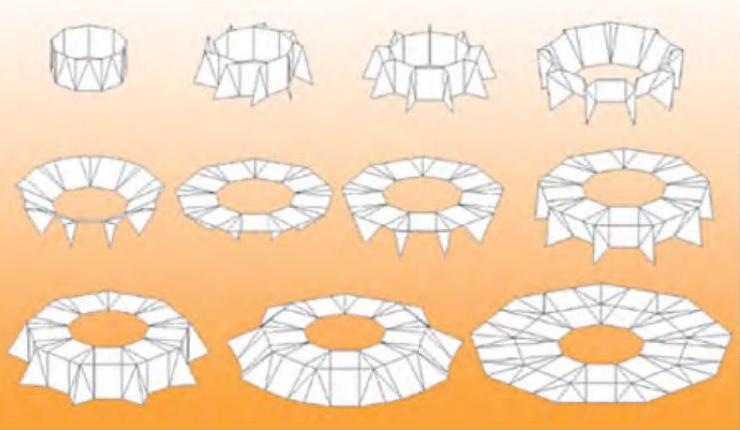
Hình 2: Kiểu gấp dù (umbrella) được ứng dụng để gấp những hình tròn lớn
thành khối hình trụ nhỏ gọn.
Mẫu thử nghiệm Eyeglass có đường kính 5m được bung ra từ hình gấp đường kính 1,5m làm việc tốt. (Hình 3)

Hình 3: Eyeglass đang trong giai đoạn nghiên cứu và nhóm này đã thực hiện thành công
mẫu thí nghiệm đường kính 5 m.
Những thứ tưởng chừng xa nhau như mặt trời và mặt trăng, vậy mà khi nhìn ra hình mẫu và vận dụng tri thức toán và khoa học để nối chúng lại với nhau, bạn sẽ đẩy tri thức con người tiến đến một bước nhảy mới. Những bài toán mà bạn phải giải đôi khi chỉ là tăng giá trị thẩm mỹ, hoặc sáng tạo thứ gì đó đẹp đẽ nhưng có lúc được áp dụng thực tiễn rất bất ngờ, kỳ lạ và … đẹp! Hẳn trước khi đọc đến đây, bạn sẽ cho là kỳ quặc khi cố gán ghép một thứ cổ xưa như origami với khoa học và công nghệ hiện nay, thế mà thật đáng kinh ngạc là không chỉ vậy, nó còn có thể cứu sống con người.
Trần Quân
TRẦN QUÂN, STINFO số 5/2015
Tải bài này về tại đây.